考试内容¶

约 2710 个字 141 行代码预计阅读时间 11 分钟

理论50min，60分单选题
实验80min
- 2道函数题（DES，AES）
- 2道程序填空（RSA，ECC）

数学基础¶

整除

若存在整数k使得b=a*k，则称a整除b，记作a|b。

素数与互素

gcd(a,b)=1

任一整数a(a>0)都能唯一分解成以下形式: \(a = p1 * p2 * p3 * ... * pt\) 其中\(p1、p2、p3、...、pt\)是素数。

最大公约数(greatest common divisor)

\(d=gcd(a,b)\)，则一定存在整数\(x、y\)使得下式成立:

\[a*x + b*y = d\]

模(mod)运算和同余(congruent)

\(a=b+n*k\)(k为整数)，我们称

a、b对于模n同余(a is congruent to b mod n)，

记作: \(a ≡ b (\bmod n)\)
- 当且仅当 \(b≡a (\bmod n)\)时, 有\(a≡b (\bmod n)\)
- 若\(a≡b\) 且 \(b≡c (\bmod n)\)，则一定有\(a≡c (\bmod n)\)
- 若\(a≡b (\bmod n)\)且\(c≡d (\bmod n)\)，则有 \(a+c≡b+d, a-c≡b-d, a*c≡b*d (\bmod n)\)

逆元
1. 加法逆元
  
  若a+b≡0 (mod n), 则称a是b的加法模n逆元，b是a的加法模n逆元。
  
  加密过程: y = (x+3) % 26 解密过程: x = (y+23) % 26， 23是3的加法逆元
2. 乘法逆元 ! ! !（代码怎么写）
  
  若\(a*b≡1 (\bmod n)\), 则称a是b的乘法模n逆元，b是a的乘法模n逆元。\(a\)的乘法逆元记作\(a^{-1}\)
  - 求解乘法逆元(扩展欧几里得)
    
    \(13 * x ≡ 1 mod(35)\)
    
    \(gcd(13, 35) = 1 \rightarrow 13*x + 35*y = 1\)
    
    \(35=2*13+9\) , \(13=1*9+4\), \(9=2*4+1\)
    
    \(1 = 9-2*4\), 再将9和4逐步由上式替换

古典密码¶

单表密码

明文密文有固定对应关系，容易被频率分析
- 加法密码（凯撒密码）
  
  解密时加上加法逆元
- 乘法密码
  
  解密时乘上乘法逆元
- 仿射密码
  
  \(y = (x*k1 + k2) \bmod n\)
  
  \(x = (y-k2)*k1^{-1} \bmod n\)

多表密码

每个明文字母可能采用不同的单表加密

\(y = (x+k_i) \bmod n\) \(x = (y-k_i) \bmod n\), \(i\) 为第i张表

Enigma

输入明文后齿轮先转动再查表：
1. 先通过接线板plugboard （打乱）
  
  \(\mathcal A \leftarrow plug[\mathcal A]\)
2. 通过右侧第一个齿轮
  
  Message Key为齿轮外部设置（外部展示的字母）
  
  Ring Setting为内部设置
  
  \(\delta = MessageKey - RingSetting\)
  
  \(\mathcal A \leftarrow (rotor[(\mathcal A + \delta)\bmod26] - \delta)\bmod26\)
3. 通过右2、3齿轮
4. 通过反射板reflector
  
  反射板输入输出不会相同，由此推出enigma明文密文不同。
5. 反向通过右3齿轮
  
  \(\delta = MessageKey - RingSetting\)
  
  \(\mathcal A \leftarrow (rotor^{-1}[(\mathcal A + \delta)\bmod26] - \delta)\bmod26\)
6. 通过右2、1齿轮，接线板
5个齿轮的进位：\(QEVJZ \rightarrow RFWKA\)

double stepping: 右2齿轮再即将进位位置，不管右1是否进位，都将带动右2旋转

Hash 函数¶

MD5

摘要，有损压缩
- \(M_1=m_0+m_1\) \(M_2=m_0+m_2\) 当\(md5(m_1)==md5(m_2)\)时，有 \(md5(M_1) == md5(M_2)\)
- 分块计算，每块64 bytes。
  
  末尾填充：0x80, (0x00), 8字节message总位数*（不含填充，小端）
  
  0x80必须有，0x00可以没有，至少需要9bytes
  
  最后一块字节数 \(\geq 56\) 时，需要开辟新的一块
  
  最后一块字节数\(\leq 55\) 时，直接在当前块填充即可
- 彩虹表破解md5
  
  计算长为n个字母的彩虹表，\(P(n)\) 表示第\(n\)种排列
```
for(i=1; i<BigNum; i++){
    n0 = rand();
    m[0] = MD5(P(n0));
    for(int j=1; j<=100; j++){
        nj = m[j-1] mod 26^4;
        m[j] = MD5(P(nj));
    }
    DB_Insert(m[100], n0);
}
```
  查找M是由什么生成的：
```
int n0;
while(!DB_Query(M, n0)){
    ni = M mod 26^4;
    M = MD5(P(ni));
}
// 拿到n0，然后按计算彩虹表流程，算出M对应的n
```

SHA

sha-1散列算法计算出来的hash值达160位，即20字节，比md5多了32位

64字节分块计算，填充方式与MD5相同

分组密码与流密码¶

电子密码簿ECB(Electronic codebook)

明文被分成长度相等的段(64 bit)，每段分别用同样方式加密。

缺点：相同的明文段密文相同。优点：可以并行处理

加密过程：\(C_j = E_k(P_j)\) （\(k\)为密钥， \(P_j\)为第\(j\)段明文，\(C_j\)为第\(j\)段密文）解密过程：\(P_j = D_k(C_j)\)

密文块链接模式CBC(Cipher block chaining)

第\(j\)块(64 bit)明文的加密与第\(j-1\)的密文相关

加密过程： \(C_j = E_k(P_j ⊕ C_{j-1})\) 解密过程： \(P_j = D_k(C_j)⊕ C_{j-1}\)

密文块反馈CFB(Cipher block feedback)

8 bit 块大小，解密时可以从密文的错误中恢复，密文某处的错误只有有限的影响范围
- 加密过程
  
  先初始化64 bit\(X_1\)
  
  \(C_j = P_j ⊕ E_k(X_j)[63:56]\)
  
  \(X_{j+1} = \{X_j[63:8], C_j)\)
- 解密过程
  
  \(P_j = C_j ⊕ D_k(X_j)[63:56]\) \(X_{j+1} = \{X_j[63:8], C_j)\)
  
  由于\(X\)每轮左移8位，所以错误的密文在8轮后就会被移走，从而从错误中恢复

表格

	加密方法	加密块大小
ECB	对明文分块加密， \(Cipher_j = Encrypt_k(\mathbf {Plain\_text_j})\)	64 bits
CBC	对明文和上一段密文共同加密，\(Cipher_j = Encrypt_k(\mathbf {Plain\_text_j}⊕ \mathbf {Cipher_{j-1}})\)，第一段用IV	64 bits
CFB	对IV加密，\(Cipher_j = \mathbf {Plain\_text_j} ⊕ Encrypt_k(\mathbf {X_j})[63:56]\) IV加密后，取高8位异或明文，更新IV的低8位	8 bits

流密码RC4

Prepare key 共256bytes

Init \(s[i] = i, i \in [0,256)\)

for(int i=0, j=0; i<256; i++){
    j = (j + s[i] + seed[i%seed_len]) % 256;
    swap(s[i], s[j]);
}

Encrypt/Decrypt (byte-wise)

对明文的处理仅仅是异或其中一个key

操作全在key上

for(int i=0, j=0; i<input_len; i++){
    j = (j + s[i%256]) % 256;
    swap(s[i%256], s[j]);
    xor_index = (s[i%256] + s[j]) % 256;
    input[i] ^= s[xor_index];
}

DES¶

密钥太短（64 bit 密钥实际56 bit被使用）

受差分分析攻击

sbox未公开，可能有后门

共16轮（左右部分分别被加密8次）（位的编号为大端）单字节，不分大小端，都是左边高位，右边低位

密钥的处理
- 原密钥64 bit -> 56 bit
  
  通过key_perm_table 函数计算得到\(\mathcal K_0\)
- 每轮加密密钥的计算
  
  左28位和右28位分别循环左移指定位数，然后查表缩减为48位
  
  \(\mathcal K_i = to48(rol(\mathcal K_0[55:28], key\_rol\_steps[i]), rol(\mathcal K_0[27:0], key\_rol\_steps[i]))\)

加密过程

先对明文打乱（initial permutation）

执行16次循环，奇数轮对左边加密
```
des_encrypt()
{
  for(i=1; i<=16; i++){
        if(i%2 == 1){ //奇数轮对左边加密
            L[i] = L[i-1] ^ f(K[i], R[i-1]); // K为第k轮的48bit密钥
            R[i] = R[i-1];
        }else{
            R[i] = R[i-1] ^ f(K[i], L[i-1]);
            L[i] = L[i-1];
        }
  }
    swap(L[i], R[i]);
}
```
- f 函数
  1. 进入明文为32 bit，先扩充为48 bit，与密钥等长
  2. 明文与密钥异或（8组，每组6 bit）
  3. 6 bit一组，共8组。分别进入sbox，获得8组4 bit结果，共32 bit
    
    sbox查询
    
    sbox[8][64] (sbox[8][4][16])，第一维即为组的编号，将每组（6bit）换算后，带入第二维。
    
    例：第零组为6'b1_0011_0, 则sbox[0][6'b10_0011]或 sbox[0][2'b10][4'b0011]
    
    sbox输入6 bit，输出4 bit
  4. 32 bit结果再次打乱
对密文反打乱（final permutation）

差分分析

差分分析对于加密轮数少的情况试用，加密轮数多了，计算量没有显著减少

假设只加密三轮，我们知道任意明文对\(L_0, R_0\) 和密文对 \(L_3, R_3\)
1. 第一轮
  
  \(L1 = L0 \oplus f(R0, K1), R1 = R0\)
2. 第二轮
  
  \(R2 = R1 \oplus f(L1, K2), L2 = L1\)
3. 第三轮
  
  \(L3 = L2 \oplus f(R2, K3) = L1 \oplus f(R2, K3) = L0 \oplus f(R0, K1) \oplus f(R2, K3) L3 = L0 \oplus f(R0, K1) \oplus f(R3, K3)\)
  
  此时只有K是未知，开始差分分析
- 改变\(L_0\)， \(R_0\)不变
  
  \(L3 = L0 \oplus f(R0, K1) \oplus f(R3, K3)\)
  
  \(\tilde L3 = \tilde L0 \oplus f(\tilde R0, K1) \oplus f(\tilde R3, K3)\)
  
  \(L3 \oplus L3 =(L0\oplus \tilde L0) \oplus (f(R0, K1) \oplus f(\tilde R0, K1)) \oplus (f(R3, K3)\oplus f(\tilde R3, K3))\)
  
  \(=(L0\oplus \tilde L0) \oplus (0) \oplus (f(R3, K3)\oplus f(\tilde R3, K3))\)
  
  \(=L0’ \oplus f(R3, K3)\oplus f(\tilde R3, K3)\)
  
  \(=L0’ \oplus sbox(E(R3)\oplus K3)\oplus sbox(E(\tilde R3)\oplus K3)\)
  
  \(sbox(E(R3)\oplus K3)\oplus sbox(E(\tilde R3)\oplus K3) = sbox(E(R3)\oplus E(\tilde R3) )\)已知
  
  这时根据各种限制条件，枚举\(E(R3) \oplus K3\) 即可

AES¶

有限域\(GF(2^n)\)

域中的元素，可表示为多项式\(f(x) = a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + … + a_1x + a_0\), 其中\(a_i \in \{0,1\}\)

也可表示为一个\(n\)位二进制数\(\{a_{n-1}, a_{n-2}, \dots,a_0\}\)。
- 加法
  
  \(a(x) + b(x) = (a(x) + b(x)) \bmod p(x)\), \(p(x)\)是不可约多项式.
  
  等同于\(\sum_0^{n-1} (a_i\oplus b_i)x^i \bmod p(x)\)
- 乘法
  
  \(a(x) * b(x) = (a(x) * b(x)) \bmod p(x)\), \(p(x)\)是不可约多项式
  
  模拟二进制竖式乘法，加法遵循有限域规则
  - 农夫算法（8 bit, mod 0x11B）
```
// input x, y (8 bit), p = x * y
unsigned int p = 0; /* the product of the multiplication */
int i;
for (i=0; i < 8; i++)
{
  if (y & 1) /* if y is odd, then add the corresponding y to p */
     p ^= x; /* since we're in GF(2^m), addition is an XOR */
  y >>= 1;   /* equivalent to y/2 */
  x <<= 1;   /* equivalent to x*2 */
  if (x & 0x100) /* GF modulo: if x >= 256, then apply modular reduction */
     x ^= 0x11B; /* XOR with the primitive polynomial x^8 + x^4 + x^3 + x + 1 */
}
```
- 逆元
  
  一个元素的加法逆元就是他本身.
  
  \(\sum_0^{n-1} (a_i\oplus a_i)x^i \bmod p(x) = \sum_0^{n-1} 0 *x^i \bmod p(x) = 0\)

加密流程

明文长度128bit，密钥长度128bit（循环10轮）、192bit（12轮）、256bit（14轮）
- 密钥生成（128bit）
  
  每16byte为一组生成，最开始16byte为种子密钥。共11组（包含种子）
  
  设\(i ≡ 0 \bmod 4\), k 是4 byte大小
  1. \(k[i] = k[i-1]\)
  2. \(rol(k[i], 1\_byte)\)
  3. \(ByteSub(k[i])\) k[i] 每个字节过sbox
  4. \(r = 2^{(i-4)/4} \bmod 0x11B\) (有限域乘法) 查表：0x01 0x02 0x04 0x08 0x10 0x20 0x40 0x80 0x1B 0x36
  5. \(k[i]\) 首字节异或 \(r\)
  6. \(k[i] \oplus k[i-4]\)
  7. \(k[i+1] = k[i] \oplus k[i-3], k[i+2] = k[i+1] \oplus k[i-2], k[i+3] = k[i+2] \oplus k[i-1]\)
- 加密
  
  第0轮，只做AddRoundKey（明文与密钥异或）
```
for(i=1; i<=key_rounds; i++)
{  
  /* 第1至key_rounds轮, 做以下步骤: ByteSub, ShiftRow, MixColumn, AddRoundKey */

  /*
    p[j] = sbox[p[j]];
  */
  ByteSub((unsigned char *)matrix, 16);

  /*
    将matrix中元素，以列主序排列 （相当于转置）
  */
  my_MixColumnInverse((unsigned char *)matrix, a, 0); /* 不做乘法, 只做矩阵行转列 */

  /*
    对矩阵每行左移 i-1 字节
  */  
  ShiftRow((unsigned char *)matrix);

  /*
    最后一轮不做乘法
  */
  if(i != key_rounds)
     MixColumn((unsigned char *)matrix, a, 1); /* do mul */
  else
     MixColumn((unsigned char *)matrix, a, 0); /* don't mul */

  /*
    明文密钥异或
  */
  AddRoundKey((unsigned char *)matrix, key+i*(4*4));
}
```
  - MixColumn
    
    取矩阵的每一列与 3 1 1 2 做多项式乘法(\(\bmod x^4 + 1\))，其中系数乘法遵循有限域规则
    
    解密乘 B D 9 E
    
    \(\left[ \begin{array}{} 2 & 3 & 1 & 1\\ 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 3 \\ 3 & 1 & 1 & 2 \end{array} \right] * \mathbf{col}\)

RSA¶

基本元素
- 大素数 \(p,q\)
- \(n = p*q\)
- \(e\) (通常为10001，应与\((p-1)(q-1)\)互素)
- \(d = e^{-1} \bmod (p-1)(q-1)\)
- 公钥 \((e, n)\)
- 私钥\((d, n)\)

加密

\(c = m^e \bmod n\)

解密

\(m = c^d \bmod n\)

明文的处理

明文\(m\)与\(n\)位数相同，且要求\(m < n\). 要不然mod后信息就没了。

通常做法是，第一个字节填0，真正的明文后移。

TODO：PKCS1

签名

创建签名：\(RSA(MD5(m), private\_key)\)

检查签名：\(RSA(Signature, public\_key) == MD5(m)\)

签名用私钥加密，公钥解密，因为需要任何人都能验证。

加密用公钥加密，私钥解密，因为只想要一个人能看到。

相关接口

// 大数相关
BIGNUM *pn;
pn = BN_new();
BN_CTX *ctx = BN_CTX_new();
// RSA 结构
RSA *prsa = RSA_new();
prsa->flags |= RSA_FLAG_NO_BLINDING;
prsa->n = pn; // 设置n
prsa->e = pe; // 设置公钥
prsa->d = pd; // 设置私钥
/*
* 密钥生成
* key_bits为n长度，是pq长度的两倍
*/
RSA *prsa = RSA_new();
prsa = RSA_generate_key(key_bits, 0x10001, NULL, NULL);
/*
* 公钥加密
* flen是要加密的明文长度
* 私钥加密同理
*/
n = RSA_size(prsa); // RSA modulus size
// 无填充，明文长度最大为RSA_size
RSA_public_encrypt(flen, bufin, bufout, prsa, RSA_NO_PADDING); // 公钥加密
RSA_private_decrypt(flen, bufin, bufout, prsa, RSA_NO_PADDING); // 私钥解密
// PKCS1 填充，明文长度最大为RSA_size - 11
RSA_public_encrypt(flen, bufin, bufout, prsa, RSA_PKCS1_PADDING); // 公钥加密
RSA_private_decrypt(flen, bufin, bufout, prsa, RSA_PKCS1_PADDING); // 私钥解密

调用大数库实现加密解密

BN_CTX *ctx = BN_CTX_new();
BN_bin2bn(bufin, n, pin); // 长为n的大端格式数bufin 转大数pin
BN_mod_exp(pout, pin, pe, pn, ctx); // pout = pin^pe mod pn 大数带余乘方
BN_bn2bin(pout, bufout)； // 大数转大端bufout

ECC¶

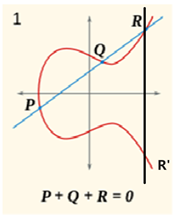
椭圆曲线的运算规则

定义\(\mathcal O\) 为零元素，\(P+\mathcal O = P, \mathcal O +P = P\)

\(P+Q=R', R+R' = \mathcal O\)

\(\exist n, \sum^n P = n*P=\mathcal O\), \(n\) 就是\(P\) 的阶。曲线上点的个数就是曲线的阶。

当\(k\)很大时，对于\(Q=k*P\), 求\(k\)很困难。

决定椭圆曲线的6要素
- 方程参数 \(a, b, p\)
  
  \(y^2 = x^3 + ax + b (\bmod p)\)
- 基点\(G\), (曲线上随便选一个)
- \(G\)的阶
- 余因子 （\(G\)的阶/基点的阶，通常为1，即基点所在子群等于原来的群）

加密解密

私钥：随机数\(d\)

公钥：\(R = d * G\)
- 加密
  
  \(r = k * G\)，不可求模
  
  \(s = m * (k * R)\) (\(s = m*(d * r)\))
  
  \(\{r.x, (s.x)\bmod n\}\)组成密文
- 解密（r.y 随便选一个）
  
  \(m = (s.x/(d*r).x )\bmod n\)

签名
- ecdsa
  - 签名
    
    \(r = ((k*G).x) \bmod n\)
    
    \(s = (m+r*d)/k\)，不可求模
  - 验证
    
    \(((m/s)*G+(r/s)*R).x == r\)
- ecnr
  - 签名
    
    \(r = (k*G).x + m \bmod n\)
    
    \(s = k-r*d \bmod n\), 可以求模，因为验证时\(s*G = (s \bmod n)*G\)
  - 验证
    
    \(r - (s*G+r*R).x == m\)

相关接口

EC_GROUP *group = EC_GROUP_new(EC_GFp_mont_method()); // 新建群
EC_GROUP_set_curve_GFp(group, p, a, b, ctx); // 设置曲线方程参数
G = EC_POINT_new(group); // 分配一个曲线上的点，仅分配空间
EC_POINT_set_affine_coordinates_GFp(group, G, gx, gy, ctx); // 根据gx, gy设置点G坐标
EC_POINT_set_compressed_coordinates_GFp(group, G, gx, 0, ctx); // 设置点G坐标(仅输入gx)
EC_POINT_get_affine_coordinates_GFp(group, T, tx, ty, ctx); // 将点坐标输出到大数
/*
* 设置group生成元，最后一个参数为余因子，一般为1
*/
EC_GROUP_set_generator(group, G, n, BN_value_one());
EC_POINT_set_to_infinity(group, T); // 将T设置为无穷远点
/*
* 点加 T = T + G
*/
EC_POINT_add(group, T, T, G, ctx);
/*
* 点乘
* r = G*m + P*n.
* 若m,p,n有null，对应的项不做计算。
* G为生成元
*/
EC_POINT_mul(const EC_GROUP *, EC_POINT *r, const BIGNUM *m, 
             const EC_POINT *P, const BIGNUM *n, BN_CTX *ctx);

EC_GROUP_free(group); // 释放群

BN_mod_inverse(tx, tx, n, ctx); // 大数带余求逆