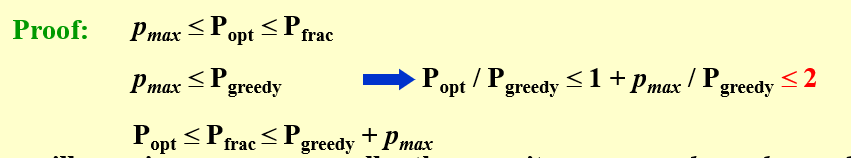Approximation¶
约 185 个字 预计阅读时间 1 分钟
Approximation ration¶
\(C/C^*\) = \(\rho (n)\) = \(1+\epsilon\)
- \(\rho(n)\) or \((1+\epsilon)\) - approximation
-
fully polynomial-time approximation scheme (FPTAS)
Polynomial w.r.t. \(\epsilon\)
Bin Packing¶
How to analyze? Construct the lower bound of each bin.
Suppose \(\sum w_i = W\), optimal solution \(C^*\). Obviously, \(C^* >= W\) (all bins are full)
-
Next Fit
\(2\) -approximation, never uses more than \(2M-1\) bins, where \(M\) is the optimal solution.
Proof:
For Next Fix strategy, each bin is at least half full.
\(W = \sum w_i \geq C * 1/2\)
\(C \leq 2W \leq 2C^*\)
-
First Fit
\(1.7\)-approximation
- Best Fit
-
Best Fit - Decreasing (Offline)
Sort. Large things first.
Knapsack Problem¶
\(2\)-approximation
If we use dp, \(O(n^2p_{max})\)
K-center Problem¶
2-approximation
We can test if \(r\) is valid by drawing circle with \(2r\)
No approximation ration less than \(2\) , unless P=NP
How to Prove an Approximation Ratio?¶
For the optimal solution \(C^*\), we consider its lower bound. \(C^* \geq X\).
Then, we associate our solution \(C\) with \(X\). (Consider the best case or constraints).
How to Disapprove an Approximation Ration Under \(\rho\)¶
Reduce an NPC problem to this problem.