SFM(Structure from Motion)

约 207 个字预计阅读时间 1 分钟

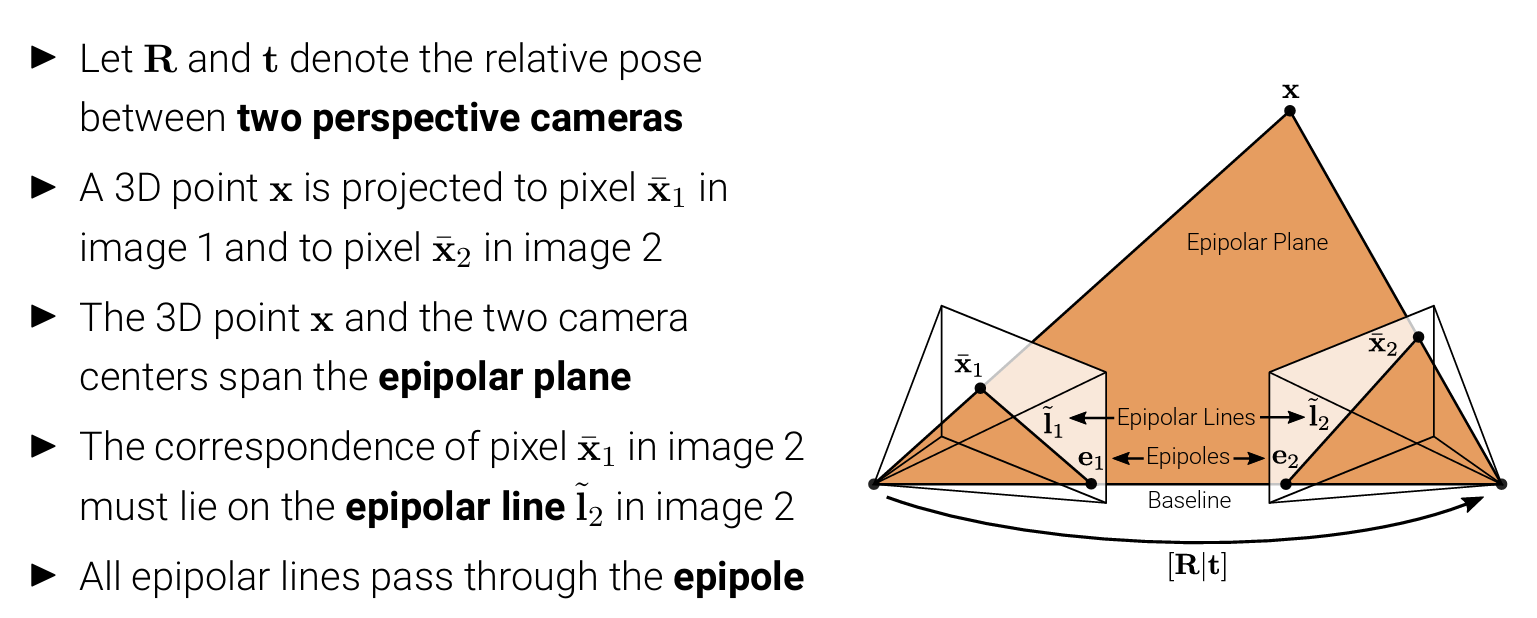
Epipolar Geometry

Goal: Recovery of camera pose (and 3D structure) from image correspondences. The required relationships are described by the two-view epipolar geometry.

To solve the essential matrix by epipolar constraint(the same as foundation matrix), we use 8-point algorithm.

One corresponding point pair provide an equation above.

1) \(N\) points pair compose a \(N * 9\) matrix \(\bf A\)

\(\bf{A = USV^T}\), where \(\bf S\) is the diagonal matrix of singular value

\(\bf {F} \in \R^{3x3}\) is the last column of \(\bf V\), that is the last row of \(\bf V^T\)

2) \(\bf F\) must be of rank 2

\(\bf{F = USV^T}\), set the third(smallest) singular value to zero, get \(\bf S'\)

Compute result \(\bf F = US'V^T\)

*. Points should be normalized s.t. \(\sum x_i = 0, \sum y_i = 0, \sum{ \sqrt{x_i^2 + y_i^2}} = \sqrt{2}\)

\(scale = \frac{\sqrt{2}}{ \bf ||\bar x||^2}\)

\(T = \left [ \begin{array}{l} scale & 0 & -sacle*\mu_x \\ 0 & scale & -scale*\mu_y \\ 0 & 0 & 1\end{array} \right]\)

\(\bf \bar x_1' = T \bar x_1\)

\(\bf \bar x_2' = T' \bar x_2\)

\(\bf F' = T'^TFT\)

Triangulation

Goal: Given the camera intrinsics and extrinsics, how can we recover 3D geometry?