Consider the metric Facility Location problem. A company wants to distribute its product to various cities. There is a set $II$ of potential locations where a storage facility can be opened and a fixed “facility cost” $f_{i}f\_i$ associated with opening a storage facility at location $i\in Ii\; \backslash in\; I$. (Sometimes we will say “facility $ii$” to mean “facility at location $ii$”). There also is a set $JJ$ of cities to which the product needs to be sent, and a “routing cost” $c(i,j)c(i,\; j)$ associated with transporting the goods from a facility at location $ii$ to city $jj$. The goal is to pick a subset $SS$ of $II$ so that the total cost of opening the facilities and transporting the goods is minimized. In short, we want to minimize $C(S)=C_f(S)+C_r(S)C(S)\; =\; C\_f(S)\; +\; C\_r(S)$, where $C_f(S)={\sum }_{i\in S}{f}_{i}C\_f(S)\; =\; \backslash sum\_\{i\; \backslash in\; S\}\; f\_i$ and $C_r(S)={\sum }_{j\in J}{\min }_{i\in S}c(i,j)C\_r(S)\; =\; \backslash sum\_\{j\backslash in\; J\}\backslash min\_\{i\backslash in\; S\}c(i,j)$. Consider the following local serach algorithm:

1. Picking any subset $SS$ of the set $II$ of facilities. This give us a feasible solution right away.
2. We then search for the local neighborhood of the current feasible solution to see if there is a solution with a smaller objective value; if we find one we update our feasible solution to that one.
3. We repeat step 2 until we do not find a local neighbor that yields a reduction in the objective value.

There are two types of “local steps” that we take in searching for a neighbor: i) remove/add a facility from/to the current feasible solution, or ii) swap a facility in our current solution with one that is not.

Which of the following statement is true?

In a character set S consisting of 5 characters, given their occurrence frequencies being 3, 5, 7, 11 and 14, the weighted average length of Huffman codes for S is:

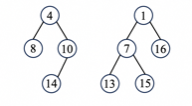
Merge the two leftist heaps in the figure. How many of the following statements is/are FALSE ?

• 8 and 10 are siblings
• 7 and 4 are siblings
• 4 and 10 have the different NPL
• along the left path from the root, we have 1, 4, 10, 16

How many of the following arguments are correct?

• For non-deterministic Turing machine, “non-deterministic” means that the operations of the machine are random, such that the results of the operations are not deterministic.
• If a decision problem A can be reduced to B, then it means that problem A is strictly easier than B in terms of computational complexity.
• A decision problem in P is also in both NP and co-NP.

If we insert $N(N⩾2)N(N\; \backslash geqslant\; 2)$ nodes (with different integer elements) consecutively to build a red-black tree $TT$ from an empty tree, which of the following situations is possible:

After inserting 15 into the Skew Heap in the figure, which of the following statements is correct for the resulted Skew Heap?

The Merging problem is to merge two non-decreasing arrays A(1), A(2), ..., A($nn$) and B(1), B(2), ..., B($nn$) into another non-decreasing array C(1), C(2), ..., C(2$nn$). To solve it in parallel, we turn it into a Ranking problem. That is, to compute RANK(A($ii$),B) and RANK(B($ii$),A) for every $1\le i\le n1\le i\le n$, where RANK($ee$,$SS$) is the position of e in S.

• The following psuedo-code computes the ranks with binary search in parallel.

  for Pi, 1<=i<=n  pardo
    RANK(A(i),B) := BS(A(i),B)
    RANK(B(i),A) := BS(B(i),A)
  

  where BS(e,S) is to find the position of e in S by binary search.
• The following psuedo-code computes the ranks in serial.

  i = j = 0; 
  while ( i ≤ n || j ≤ m ) { 
    if ( A(i+1) < B(j+1) )  
        RANK(++i, B) = j; 
    else  RANK(++j, A) = i; 
  }
  

How many of the following statements are True?

• For binary search parallel ranking, $T(n)=O(\log n)T(n)\; =\; O(\backslash log\; n)$, $W(n)=O(n)W(n)\; =\; O(n)$
• For serial ranking, $T(n)=O(n)T(n)\; =\; O(n)$, $W(n)=O(n)W(n)\; =\; O(n)$
• Given a solution to the ranking problem, the merging problem can be solved in $O(1)O(1)$ time and $O(n)O(n)$ work.

In a binomial queue, we donote the total number of the nodes at even depth and odd depth as $N_{1}N\_1$ and $N_{2}N\_2$, respectively (the root is defined to be at the depth 0). Which of the following statements is FALSE?

Consider the following function, where the time complexity for function calc() is $O(1)O(1)$.

void fun(int l, int r) {
    if(r-l+1<=1234) return;
    int m=(l+r)/2;
    int m1=(l+m)/2, m2=(m+1+r)/2;
    fun(l, m);
    fun(m1+1, m2);
    for(int k=1;k<=r-l+1;k++)
        for(int i=1;i<=r-l+1;i++)
            for(int j=l;j<=r;j+=i)
                calc(j, i);
    fun(m+1, r);
    fun(m1+1, m2);
}

Assume the initial input is l=1, r=N, What is the running time of this function? Your answer should be as tight as possible.

For the Maximum Finding, how many of the following statements are True?

• Replace “+” by “max” in the parallel summation algorithm, we get an algorithm with $T(n)=O(\log n)T(n)\; =\; O(\backslash log\; n)$, $W(n)=O(n)W(n)\; =\; O(n)$.
• There exists a parallel algorithm solving the problem in constant time.
• With high probability, parallel random sampling algorithm can run with $O(\log n)O(\backslash log\; n)$ work load.
• By adjusting the partition to $\sqrt{n}\backslash sqrt\; n$ with a parallel divide and conquer paradigm, we can achieve $T(n)=O(\log \log n)T(n)\; =\; O(\backslash log\backslash log\; n)$, $W(n)=O(n)W(n)\; =\; O(n)$

To find the $kk$th smallest number in a set $SS$, randomized quick selection algorithm works in the following way:

1. If $\mathrm{\mid }S\mathrm{\mid }=1|S|=1$, then $k=1k=1$ and return the only element in $SS$.
2. Randomly select a central splitter $p\in Sp\backslash in\; S$, which is a pivot that divides the set so that each side contains at least $\mathrm{\mid }S\mathrm{\mid }\mathrm{/}4|S|/4$ elements.
3. Partition $S-\{p\}S-\backslash \{\; p\backslash \}$ into $S_{1}S\_1$ and $S_{2}S\_2$, as was done with quicksort.
4. If $k\le \mathrm{\mid }{S}_1\mathrm{\mid }k\backslash le\; |S\_1|$, recursively find the $kk$th smallest number in $S_{1}S\_1$. If $k=\mathrm{\mid }{S}_1\mathrm{\mid }+1k=|S\_1|+1$, return the pivot as the answer. Otherwise, recursively find the $(k-\mathrm{\mid }{S}_1\mathrm{\mid }-1)(k-|S\_1|-1)$st smallest number in $S_{2}S\_2$.

If $\mathrm{\mid }S\mathrm{\mid }=n|S|=n$, then the best upper bound of the expected time complexity of this algorithm is:

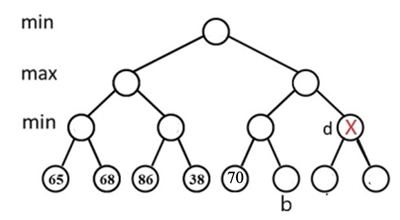
Given the following game tree, node $dd$ will be pruned with $\alpha -\beta \alpha -\beta$ pruning algorithm if and only if _____.

In external sorting, suppose we have $nn$ runs of lengths $2^0,2^1,\dots ,2^{n-1}2^0,\; 2^1,\; \backslash ldots,\; 2^\{n-1\}$, respectively. To obtain the minimum merge time, which of the following statement is FALSE?

A sum list L is a data structure that can support the following operations:

• Insert (x, L): insert the item x into the list L. The cost is 1 dollar.
• Sum(L): sum all items in the list L, and replace the list with a list containing one item that is the sum. The cost is the length of the list |L| dollars.

Now we would like to show that any sequence of Insert and Sum operations can be performed in $O(1)O(1)$ amortized cost per insert and $O(1)O(1)$ amortized cost per Sum. Which of the following statement is TRUE?

We all know how to use the binary search method to find a value in a monotonic array. As an extension, we will use the ternary search method to find the extremum in a quadratic-function-like array. Formally, for an array $aa$, let $kk$ be the position of its extremum. Then we have either or . Apply the ternary search method to locate $kk$. For a given interval , locate the two trisection points in $[l,r][l,r]$ as $m1=l+\lfloor \frac{r\text{−}l}{3}\rfloor m1=l+\backslash lfloor\backslash frac\{r-l\}\{3\}\backslash rfloor$ and $m2=l+\lfloor \frac{2(r\text{−}l)}{3}\rfloor m2=l+\backslash lfloor\backslash frac\{2(r-l)\}\{3\}\backslash rfloor$. Assuming we are looking for the minimum value, which of the following pieces of code can correctly narrow down the target interval?

Which of the following is NOT an element of Greedy strategy?

When searching for the keyword "game theory" on Google, the first four results returned are as follows:

Now if we construct an inverted file index for the results shown above, ignore case（忽略大小写）and do word stemming, please fill in the blanks in the inverted file index (not complete) below:

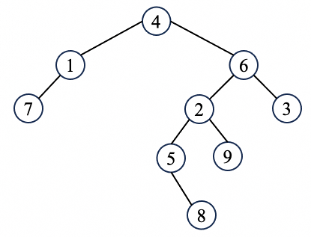
For the result of accessing the keys 2 and 3 (in order) of the splay tree in the figure, which one of the following statements is FALSE ? (Note: the numbers are the indices of the nodes, not the key values.)

Which of the following statements about binomial queue is FALSE?

Consider the 0-1 knapsack problem with object weights $ww$, profits $vv$, and total weight limit $BB$ (means that $ww$ of any object is no larger than $BB$.). In the class, we have learned that combining the greedy algorithm on maximum profit $vv$ and maximum profit-weight ratio $v\mathrm{/}wv/w$ leads to an approximation algorithm which always produces a solution no less than 1/2 of the optimal solution. Now let us consider the following simplified greedy algorithm. The algorithm first conducts the following sorting w.r.t. profit-weight ratio:

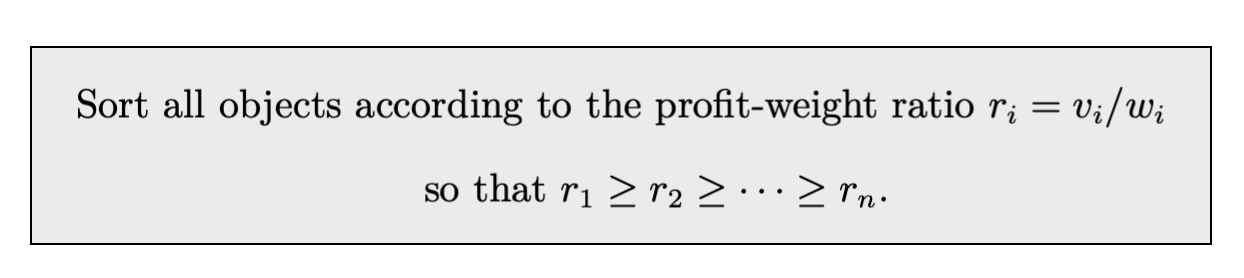
Let the sorted order of objects be $a_1,\dots ,a_{n}a\_1,\; \dots ,\; a\_n$. The next step is to find the lowest $kk$ such that the total weight of the first $kk$ objects exceeds $BB$. Finally, we pick the more valuable of $\{a_1,\dots ,a_{k-1}\}\backslash \{a\_1,\; \dots ,\; a\_\{k-1\}\backslash \}$ and $\{a_k\}\backslash \{a\_k\backslash \}$ as the final solution. Then which of the following arguments is correct: