NP Completeness

约 271 个字 预计阅读时间 1 分钟

Decision Problems

The following discussion are all around decision problem.

An optimization problem can be converted to decision problem.

Formal Language

A language \(L\), consisting instances of a problem.

e.g. In Hamilton cycle problem, \(L\) = all Hamilton graphs.

\(x \in L\) in one of the Hamilton graph.

Accept

An algorithm \(A\) accept language \(L\), if it accepts all \(x \in L\).

An algorithm \(A\) decides language \(L\), if it accepts \(L\) and correctly rejects \(x \notin L\). (some algorithm will enter infinite loop thus can only accept but not decides \(L\))

Verify

Certificate \(y\). (Possible solution to prove \(x \in L\))

An algorithm \(A\) can decides \(L\) if \(\forall x\in L, \exist y, A(x,y) = 1\).

Complexity class NP

Those \(L\) that can be verified in polynomial time.

Those \(L\) can be solved in polynomial time in non-deterministic machine

NPC

\(\forall A_{NP} \rightarrow_{polynomial reduce} B_{NPC}\)

If we want to prove problem \(A\) is NPC, then \(A\) should be on the right side.

Reduce means no harder than.

co-NP

\(\bar L \in NP\)

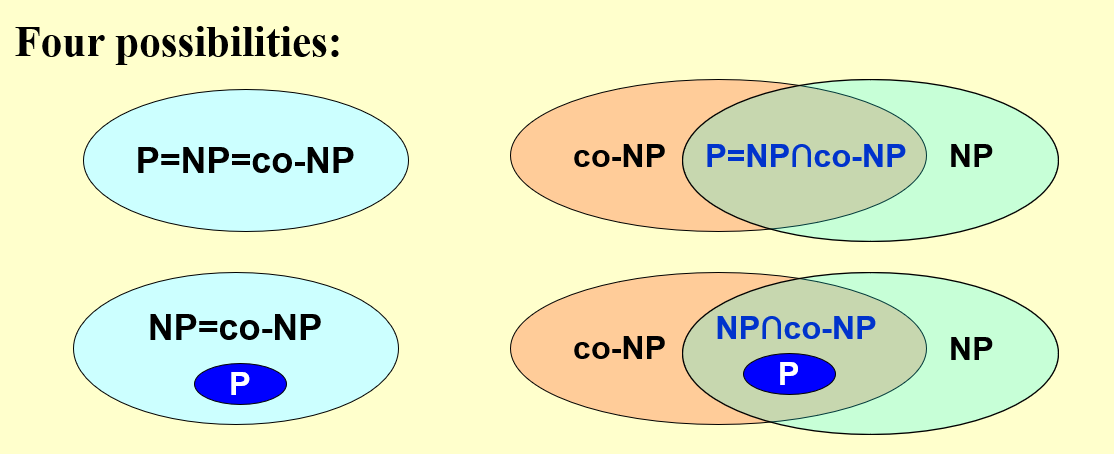
Relations

\(P \subset NP, P \subset co-NP\) always holds.

Not decided yet:

1. If \(L \in NP\), \(\bar L \in NP\) ?

   If \(L \in NP \rightarrow \bar L \in NP\) holds, this means \(L \in NP \iff L \in co-NP\)

2. \(P = NP\) (\(P = NP \cap co-NP\)) ?

Classical NP-problems

• Clique problem

  Find a complete subgraph with K vertices

• Vertex Cover problem

  Find a vertex set with K, covers each edge.

• Circuit SAT

• Hamilton cycle

  Travel each node once

• TSP

  If the cost of TSP doesn't satisfies triangle inequality, there are no approximation algorithms.